| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- 피보나치함수 예제
- git 연동
- 재귀함수 예제
- 피보나치함수
- oracle group by
- tomcat log
- katalon 사용법
- katalon
- Katalon Recorder 사용법
- 국세청 해외주식 양도세 신고방식
- recursion example
- js 자동완성
- 한국투자증권 해외주식 양도세
- 최대공약수 예제
- 톰캣 실시간 로그
- 테스트 자동화
- 해외증권 양도세 한국투자증권
- 한국투자증권 양도세 신고
- CSTS 폭포수 모델
- 홈택스 해외주식 양도세
- 재귀 예제
- katalon xpath
- 피보나치 예제
- 주식 양도세 신고방법
- java.sql.SQLSyntaxErrorException
- katalon 자동화
- javascript 자동완성
- katalon 비교
- 해외주식 양도세 신고
- bfs 미로탐색 java
- Today
- Total
엄지월드
그리디 알고리즘 본문
그리디 알고리즘이란? 탐욕 알고리즘이라고 불리는 그리디 알고리즘은 현재 상황에서 가장 최선의 선택을 하는 기법이다.
그리디 알고리즘은 빠르지만 최적해를 보장하지는 못하며, 최적해에 가까운 값을 구하는 경우 사용 가능하다고 한다.
만약, 딥러닝에 관심이 있는 사람이라면 딥러닝 알고리즘 개발할 때에 사용된다고 하니 잘 익혀두는게 좋을듯하다.
그러면 어느 상황에서 그리디 알고리즘을 사용해야 할까?
아래 두 가지 조건에 해당하면 적용이 가능하다.
1. 탐욕적 선택 특성(Greedy choice property)
- 지금 선택이 다음 선택에 영향을 주지 않는 경우
- 즉, 무슨 말이냐면 아래 그림처럼 B를 선택했을 때에와 C를 선택했을 때에 선택권이 달라지면 안된다.

2. 최적 부분 구조(Optimal substructure)
- 전체 문제의 최적해는 부분 문제의 최적해로 이루어지는 경우
- 즉, 아래 그림과 같이 서울에서 대구를 거쳐 부산까지 가는 최단 경로는 각각의 부분인 1)서울에서 대구까지 가는 최단 경로와 2)대구에서 부산까지 가는 최단 경로 문제의 해결 방법의 합이다.
따라서 최적 해결 방법은 부분 문제에 대한 최적 해결 방법으로 구성된다. 이러한 구조를 최적 부분 구조라 한다.

[문제 1]
그러면 무슨 문제들이 존재할까? 예로 들면, 대표적으로는 거스름돈 문제가 있다.
https://www.acmicpc.net/problem/5585
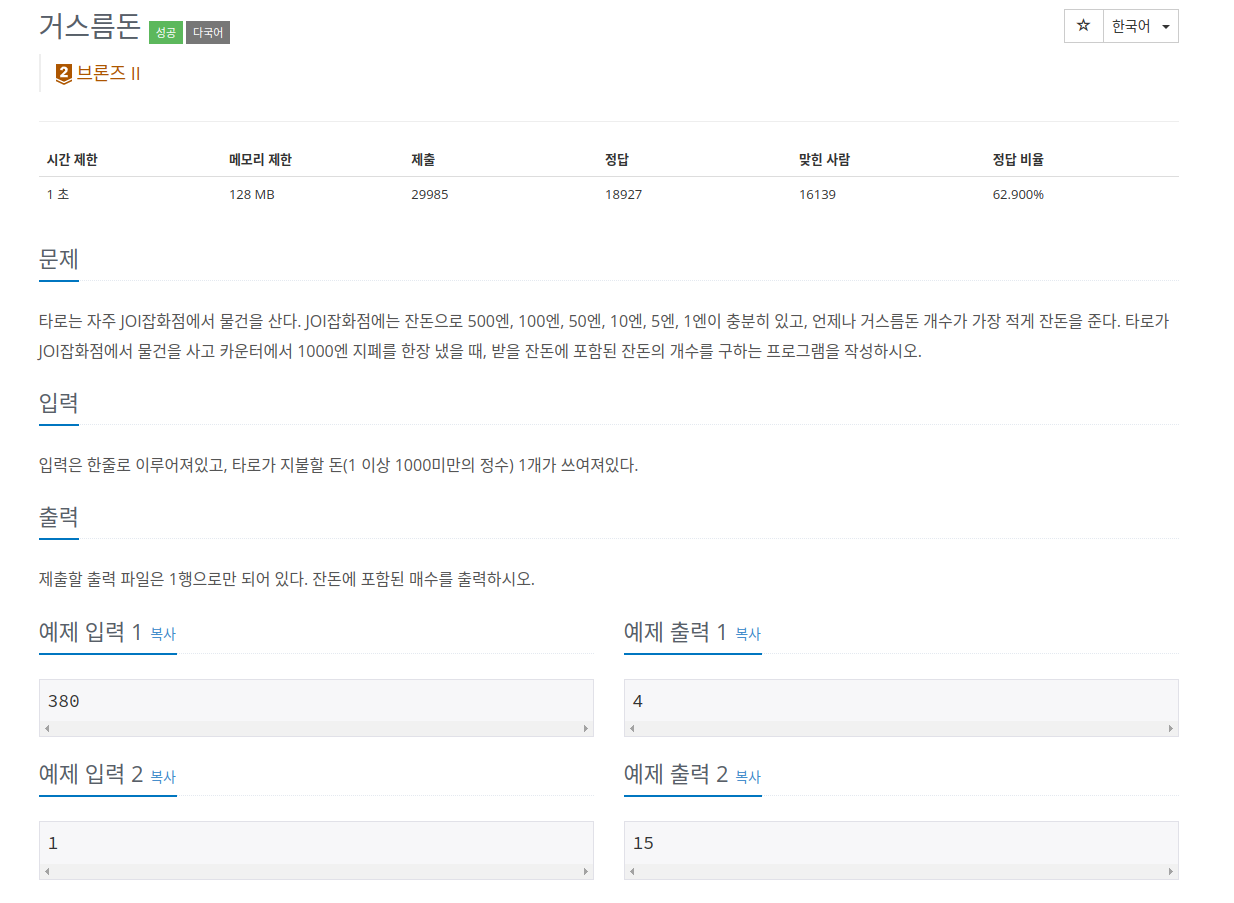
접근 방법은 입력받은 거스름돈을 기준으로 해서 가장 큰 값인 500엔부터 1엔까지 비교하면 가장 적게 잔돈을 주도록 구성할 수 있다.
[문제 2]
조금 더 머리를 굴려볼까? 추가적인 그리디 알고리즘 문제로는 회의실 배정 문제가 있다.
https://www.acmicpc.net/problem/1931
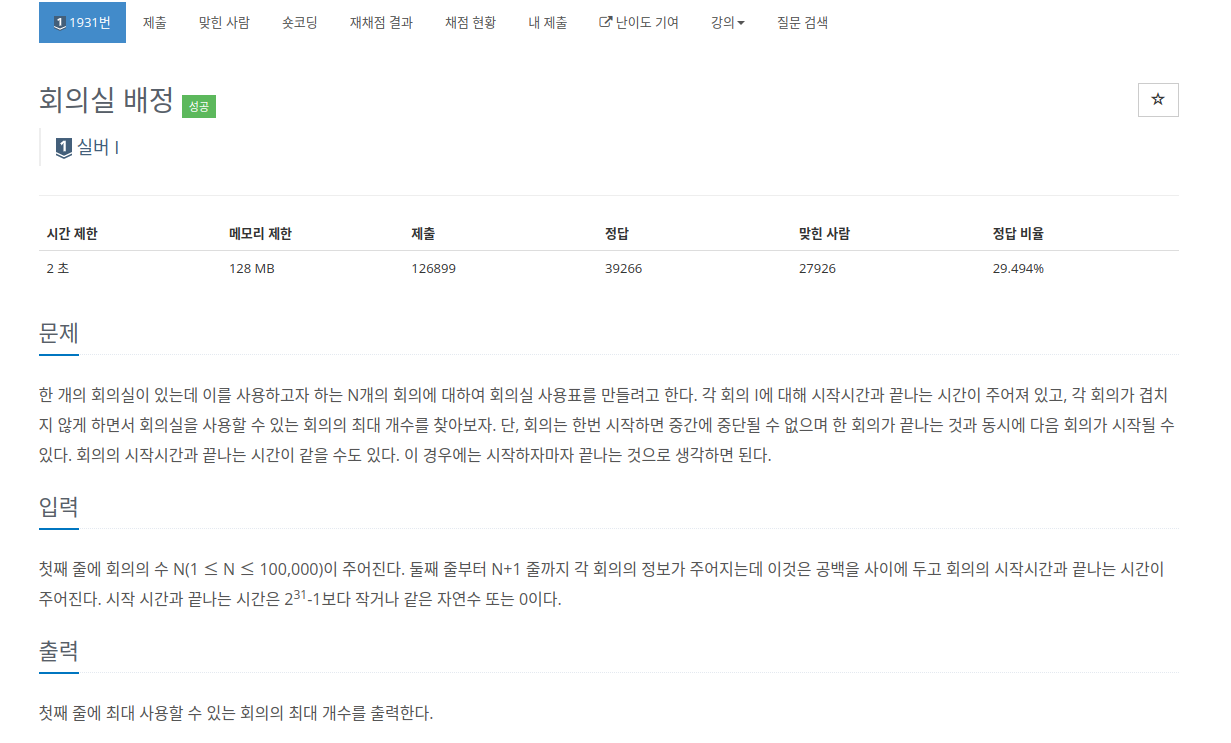

접근 방법으로는 시작 시간과 종료시간을 데이터로 입력 받기 때문에 가장 먼저 시작하는 회의실 기준으로 정렬을 진행한다.
1 4
3 5
0 6
5 7
3 8
5 9
6 10
8 11
8 12
2 13
12 14
그래서 사용되는 회의실은 (1,4) -> (5, 7) -> (8, 11) -> (12, 14)로 4개이다.
접근 방법은 정렬을 진행하고 나서 가장 먼저 회의실을 선택하고, 그 이후에는 시작 시간이 이전 종료 시간보다 더 늦은 것을 잡아서 갯수를 세어주면 된다.
'알고리즘' 카테고리의 다른 글
| [백준] 2178 미로 탐색 (BFS) (0) | 2022.07.27 |
|---|---|
| 기술면접 준비 (0) | 2022.07.08 |
| 팰린드롬 (0) | 2022.06.17 |
| 순환(Recursion)의 개념과 기본 예제2 (0) | 2018.09.16 |
| 순환(Recursion)의 개념과 기본 예제1 (0) | 2018.09.16 |

